Dopo numerosi viaggi nel mondo Arabo, Leonardo Fibonacci detto Leonardo Pisano (Pisa 1175 -1240 ) pubblicò nel 1202 la sua opera più importante: il Liber abaci; Il libro diffuse il sistema decimale nel mondo occidentale, e portò in Europa una ventata di nuove conoscenze matematiche.

Con il Liber Abaci, Fibonacci introdusse la serie numerica omonima, che si può ritrovare in natura in numerosi esempi (tra i quali l'approssimazione del Rapporto Aureo, la struttura dei grappoli d'uva, e così via).

La serie di Fibonacci è una successione di interi che inizia dalla coppia di numeri (1,1) in cui l'elemento successivo è calcolato come somma degli ultimi due.
Facciamo un esempio:
Il primo numero è 1, e il secondo numero è 1.
Il terzo numero corrisponde a:
2= 1 + 1
Il numero 2 è dato dalla somma dei numeri 1 (primo numero) e 1 (secondo numero).
Per il quarto numero è dato dalla somma del secondo numero più il terzo numero e cioè:
3=2+1
Il quinto numero è dato dalla somma del quarto numero più il terzo numero (in sintesi, dalla somma degli ultimi due numeri), e quindi:
5=3+2
e gli altri di seguito:
8=5+3
13=8+5
21=13+8
...............
..............
..............

Quindi il primo elemento della serie è Fib(0) = 1, mentre il secondo elemento è Fib(1) = 1.
Il terzo elemento sarà dato dalla seguente:
Fib(2) = Fib(0) + Fib (1) che in questo caso risulta così:
Fib(2) = 1+1 = 2
Quindi in generale possiamo dire che:

Fib (n) = Fib(n-1) + Fib (n-2) con n>1

Il valore della funzione Fib è definito in termini della funzione stessa, e per tale motivo la funzione è detta ricorsiva.

FIBONACCI E IL TEST ALU C++.

Per chiarire ulteriormente il codice del programma descritto in questo articolo cerchiamo di capire cosa succede se inseriamo un valore di N uguale a 3 (di default il valore di N è uguale a 42).

Dalla figura successiva appare evidente che la funzione fib(N) termina quando incontra i casi base zero, e uno. Nel caso fib(3), il nostro programma C++ restituisce il valore 1 in caso di fib(1), e il valore 0 in caso di fib(0), e quindi fib(3) è uguale a 2.

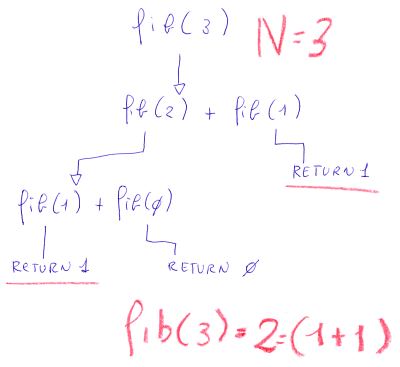
GRAFICO LA SERIE DI FIBONACCI.

Per N uguale a 5, fib(5) è uguale a 5 (provate a verificare tale valore), sapendo che fib(5) = fib(4)+fib(3), e a sua volta fib(4) è uguale a fib(3)+fib(2), mentre fib(3) = fib(2)+fib(1) e via dicendo.

Menu Sezione/Pagina Precedente/Pagina Successiva/Torna alla Homepage

Sito:www.megaoverclock.it